Tags

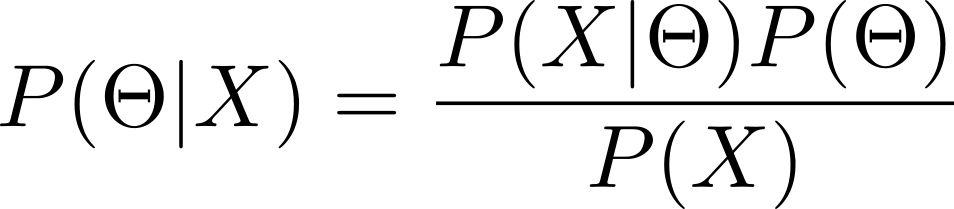
Bayesian methods make use of Bayes’ theorem to perform statistical inference. Bayes’ law states that a conditional probability can be decomposed in the following way: \[P(A | B) = \frac{P(B|A) P(A)}{P(B)}\] where \(A\) and \(B\) indicate two events. The following terms are assigned to each of the quantities: \(P(A|B)\) is the posterior probability \(P(B|A)\) is the likelihood of \(B\) given \(A\) \(P(A)\) and \(P(B)\) are the marginal probabilities for \(A\) and \(B\), respectively In statistical modeling, another parameterization is typically used.

Although all posts in this blog are somehow concerned with analyzing data, not all of them lead to new insights. Posts in the analysis series exhibit at least one of the following two properties: The analysis of the data is comprehensive (i.e. involving multiple approaches) The analysis leads to new insights Posts in the analysis series The following posts are concerned with the analysis of individual data sets.

In contrast to independent measurements, matched data consist of measurements that should be considered together. For example, matching can be used in clinical studies. Here, patients that exhibit similar characteristics are paired in order to remove confounding effects. Matched data can also arise naturally when multiple measurements are performed on the same entity. For example, matched data can arise when a clinical marker is measured once before and once after a treatment intervention.